量子論～量子力学の歴史：ニュートン・アインシュタイン～現在まで理系以外の方でもわかるようにこの記事1本でわかりやすく解説！

最近、量子論、量子力学といった言葉を聞かない日はないのではないでしょうか？
でも、名前は聞いたことあるけど全然わからん！というのが実際のところだと思います。

この記事では、量子論の歴史をやさしくやさしく解説します。

なぜ歴史から扱うかって？
なぜなら、量子論とは何か、を知るには歴史から入るのがいちばんだからです。

量子論の歴史は世界最高の英知を持った人々の苦闘の記録です。
彼らの見事な発想や血のにじむような努力は、我々の参考になることが多いです。
また、量子論の進歩で我々の社会は大きく変化しました。

実際、スマホは、量子論がなければ作れなかったのです。

また、量子論が現れて我々の認識も進歩してきました。
たとえば、人のいない山奥で木が倒れたとき、音はするのか？
これは昔の禅問答ですが、こうした議論が科学的に議論できる土台がそろったのです。

このように、現代社会そして将来の社会に、量子論は大きく関係しています。
量子論は、現代人が知っておくべき常識の1つなのですよ。

本記事では、下記の順番で量子論の歴史を解説します。

めくるめく科学の世界を、どうか、ゆっくりとおたのしみください。

量子論誕生の背景（～1900年まで）

量子論とは？

そもそも量子論とはなんでしょうか？

量子論または量子力学は、ものすごく微小なミクロの世界を解明するための理論なのです。

私達は、世界は物質から構成されている（この表現が突き詰めると微妙なのですが・・・）と学びます。
そして、その物質は分子、そして、更に原子にまで細分化され、そして、原子の周囲には電子が周回しているとされます。

その原子核をピーナッツサイズに例えれば、原子は野球場ほどのサイズ。

このような、ものすごく微小なスケールの世界が舞台になっています。
さらに言えば、原子核がピーナッツ、原子が野球場ならばその間はすっからかんの空洞なのでしょうか？
このようなすっからかんの原子の集合体が分子であり、物体であるということになるのです（驚）。

このように、微小なスケールの世界を通して理解を深めていくと、我々が知っているマクロの世界と何かが大きく違っているのでは？
そういう思索に至ることになります。

さらに、微小なミクロの世界では、連続なことはなく、すべてが不連続になっています。
もともと「量子（quantum）」とは、不連続という意味なのです。

微小なミクロの世界は”あいまい”なのです。

”あいまい”っておかしいじゃないですか。
不確かなままにしないで、キッチリして下さいよ。

こう思うかもしれません。
でも、”あいまい”なのです。

あいまいで、キッチリできない、というのが量子の世界なのです。

我々のよく知っているマクロの世界の物理法則である古典物理学（中学高校で習ったアレです）では、微小なミクロの世界は説明ができないのです。

どうすれば説明ができるのか？

多くの天才たちが頭を絞りました。
膨大な計算をしました。
精密な実験をしました。
しかも、考え方自体を入れ替える必要もあったのです。

この苦闘の歴史が量子論の歴史なのです。

量子論が作られたきっかけ

19世紀末のことです。
物理学は終わった、と思われていました。

ニュートン力学ですべての物理現象の説明が付く、と信じられていたのです。

地球が太陽の周りを回ることも、リンゴが木から落ちることも、すべて説明できたのです。
ニュートン力学を使えば、大砲を撃って敵の陣地へ正確に着弾させることもできました。

ニュートン力学は万能でした。
物理学者はもう研究することがない、物理学者は失業する、とさえ思われていました。

光の謎

ただ、この古典物理学の世界でもまだ未解決のテーマが残っていました。
その一つが光です。

光というものがよく分からなかったのです。
同様に、原子の中もよく分かりません。

• そんなはずないだろ！
• 波であり、粒であるなんて！
• どっちかのはずじゃないか？

ただ、量子論が誕生する前の時代はまだ仕方ないこともありました。
調べるのに足るだけの機器や方法がわからなかったからです。

光のことも原子のことも、新しい実験方法を考案して、実験の精度がもっともっと向上すればニュートン力学で説明が付く・・・、と物理学者たちは信じていたのです。
なにぜ、物理学の世界は目に見える現象がすべてなのです。実験結果がすべてということです。

ところがです。

その結果が、

• 「光は波である」という「実験結果」
• 「光は粒子である」という「実験結果」

どっちもオッケー！
なんていうあやふやなものだったらどうでしょうか？

量子論はここからはじまりました。

光とは – 粒子 VS 波動論争

ヤングは光は波と、そして、ニュートンは粒だと考えた

19世紀末の時点で、いちばんよく分からないとされていたのは光でした。

「光は波なのか？粒子なのか？」
この問題の発端はアイザック・ニュートン（イギリス）の時代（1600年代～1700年代）に遡ります。

ニュートンの時代、すでに、「光は波である」という研究者も実は結構いました。
代表的なのはオランダの物理学者、クリスティアン・ホイヘンスです。

一方、『プリンキピア』（1687年）を発表しすでに学者としても大御所となっていたニュートンはもう一つの著書『光学』（1704年）で「光は粒である」説を自説とします。

ニュートンは光の研究としても第一人者で光が7色に分かれることを発見しました。
そして、その大御所のニュートンが、「光は粒子」だと言ったのです。
でも、当時、それを証明する方法は見つからなかったのです。

先ほど言ったように正解は、「光は、波でもあり、粒でもある」でホイエンスもニュートンいずれにも一理あるのです。
ただ、18世紀にかけてニュートンの光の粒子説が幅を利かせ波動説は誤りだとされました。

それから100年後・・・。

これまで行われていた光に関する実験に大幅な改良がなされました。
そして、実験の結果から光の正体を探ることにしたのです。

光の干渉

19世紀の初頭、トマス・ヤング（イギリス）はつぎのような実験をしました。

1つの光源を用意して、すぐ近くに1本のスリット（切れ込み）が入った遮光板をたてます。そして、その向こうに少し感覚をあけて2本の平行なスリットが入った遮光板を立てて、その後ろに、光を映し出すスクリーンを設置しました。

さて、皆さんはこの実験どうなると思いますか？
ニュートンが言うように「光が粒子である」とするならば、光はただ直進してスクリーンには明るい2本の線が出てくるはずです。

ところがです・・・・。
実験を行ってみると予想外の結果となりました。

壁には、光の縞模様ができました。
つまり、スクリーンには明るい線（明線）と暗い線（暗線）が交互に何本も観測されたのです。

これを干渉縞（かんしょうじま）といいます。
干渉縞が発生するのは、波の干渉によって生じる現象です。
2つの波が重なり合って、強くなる場所と弱くなる場所が生じます。
その結果、縞模様ができるのです。

同じような現象は水の波でも確認できます。
静かな池に2つの波を起こせば、干渉による波の強弱を見ることができますよね。

こうして、ニュートンの権威によって200年余り続いた「光は粒子だ」理論が破れ、「光は波だ」理論が優位になります。
（ただし、当初ヤングはニュートンの権威を傷つけたとかなり叩かれたそうです。）

レイリー・ジーンズとヴィーンの公式

光が波ならば、振動数と強度で光を表すことができます。
振動数が光の色であり、強度が明るさなのです。

光のエネルギーは振幅に比例しています。

時代は19世紀～20世紀へと移り変わる次期。
当時、ドイツでは製鉄業の発展をうけて、溶鉱炉の効率的な管理が必要とされていました。

そのために大事になるのは、炉内の温度を正しく測定すること。
ただ、現実問題として数千度に達する炉内を測れる温度計はありません。

そこで論理的に温度を推測する方法が模索されました。
鉄は熱されていくと、初めは赤色で、温度が上がると次第に白熱色になっていきます。
これは、加えられた熱エネルギーによって、物質を構成する電子などが振動して、その振動に応じた波長の電磁波（光）を放射するからです。

つまり、この現象（物体の温度と色（光））にも振動数（波動）と強度が関係しているということです。

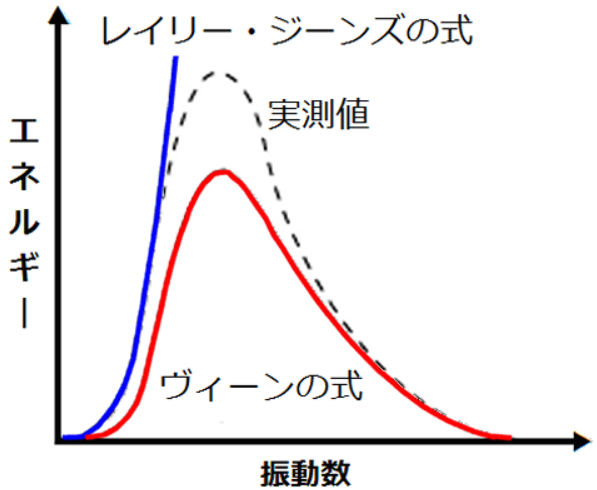
1896年ドイツの物理学者ヴィルヘルム・ヴィーンがヴィーンの公式を発表します。
短い波長（高振動数）の領域では、実験と計算式がかなり正確に一致しました。

また、1900年イギリスの物理学者レイリー卿が別の式を発表。
さらに、イギリスのジェームズ・ジーンズの指摘を反映し、式は更に改善されレイリー・ジーンズの公式と呼ばれる式が誕生しました。

これにより、低振動数の領域で合致する式が誕生しました
（逆に、高振動数の領域にはあわなかった）。

プランクの量子仮説と量子論の誕生

マックス・プランク

さて、レイリー・ジーンズとヴィーンの公式という2つの式が存在します。

これらに式は半分ずつ現実とマッチしている。
これは不自然です。なんとか1つにまとまらないかな？

2つの式を1つにまとめて、白熱色になる現象を表す式を作ったのがマックス・プランク（ドイツ）です。
かなり強引に、1つの式にまとめたのです。
しかし、計算結果は、あらゆる振動数の領域で観測データと合致しました。

やったー＼(^o^)／

結果として、ウイーンの式にマイナス1を付け加えれば1つの式になりました。
都市伝説では、プランクの学生が、「先生、マイナス1を付け加えれば一致しますよ」と見抜いたことになっています。

エネルギーの最小単位（量子）概念の登場

プランクの次の仕事は、自分が作った式の意味を調べることでした。
彼は強引に2つの式をまとめました。でも、それだけでは納得しません。物理学者ですから、自分の作った式の理論的な意味を探求したのです。

プランクは、自分の式が成立するには、「振動子が吸収・放射するエネルギーは離散的な値しか取れない」という一見不可解な法則があるとしか説明が行かないことを突き止めます（変な表現ですね（笑）。）

つまり、光のエネルギーが連続ではなくて不連続だと仮定すると式に意味が出ることを発見しました。

プランクはここから、「一つの振動子が受け取ったり外に出したりするエネルギーには、それ以上細かく分割できない最小単位がある」という仮説を立てます。

この最小単位のアイデアこそが「量子」です。

プランク定数の誕生

プランクは、ここでエネルギー量子（不連続を表す数字）を表現するために途方もなく小さな単位を考えました。

この不連続を表すとても小さな単位こそが、現在、プランク定数hと呼ばれているものです。
これが量子論の事実上のスタートでした。

それぞれの振動子を特徴づけるのは、固有の振動数です。
ある振動数のエネルギー量子を表現する時は、振動数と関連付ける必要があります。

そこで、エネルギーの離散的（不連続）な変化から、エネルギー量子の値（E）を調べ、これを振動子の固有振動数vで割りました。すると、ありえないくらい小さな数字が出てきます。

この定数をhの記号で表すと、エネルギー量子Eは、

の式で表現されます。

このh（プランク定数）は現在、6.62607015×10のマイナス34乗として表現されています。

ちなみにプランクは、式に意味を与えるために不連続を”仮定”したのです。
ただ、まさか、本当にエネルギーが不連続であるとは思いませんでした。

量子論のスタート

こうして、エネルギー量子Eはhvの形で記述されることになりました。
つまり、vという振動数を持った振動子は、hvの整数倍のエネルギーでしか、吸収も放射もできないということです。

プランクの量子仮説は非常に画期的なものでした。

従来は、エネルギーなどの物理量は連続的に変化するものとされていました。
しかし、物理量の変化が連続的に見えるのは、「プランク定数hの分の段差が小さくて認識できない」からに過ぎないことがわかったからです。

プランク自身はここまで大きな発見をしたものの、自分の発見した量子の概念がしっくりこなかったようです。

アインシュタインと光電効果

アルバート・アインシュタイン

こうして、「光は波である」と広く信じられるようになりました。
干渉という波特有の性質を持っているのですから、これ以上確かな証拠はありません。

ただ、プランク自身も自分の発見に懐疑的でありこのままですと量子論はここまで発展しなかったと思われます。
しかし、プランクの量子仮説の数年後、もうひとりの天才が登場します。

そう。ドイツ出身の天才科学者、アルバート・アインシュタインです。
彼が1905年に発表した「光量子論」において、光に代表される電磁波はそれ自体が量子でできている、と発表したのです。

光自体が量子である

光が波動である仮説において、ただ1つだけ説明のつかない現象がありました。
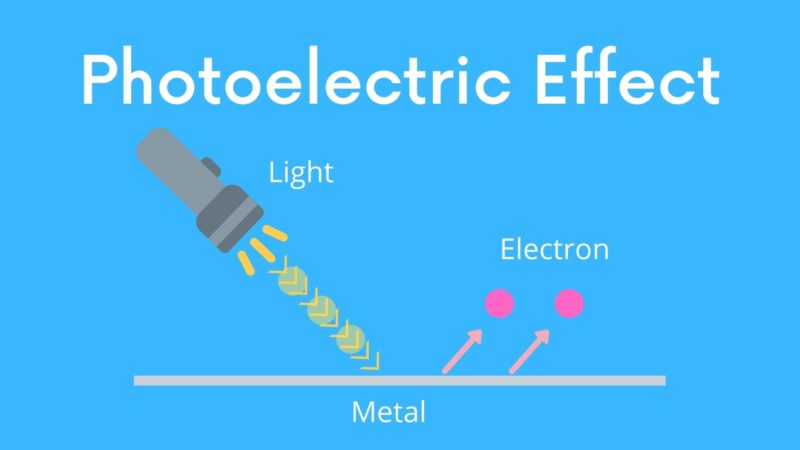
それが光電効果です。

金属板に光を当てます。金属板の中の電子は、光からエネルギーを貰って金属板から飛び出します（上記図参照）。
これを光電効果といいます。

強い光を当てれば（つまり光のエネルギーを強くすれば）、飛び出る電子も大きいエネルギーをもっているのです。

飛び出した電子の持つエネルギーは光の振動数に関係することが実験で分かっていました。

これが不思議なことでした。
もし光が波ならば、光のエネルギーは振幅に比例しています。振動数を一定にしたまま振幅を大きくすれば（つまり光のエネルギーを大きくすれば）、飛び出る電子のエネルギーも大きくなるはずです。

でも、実際には、どんなに振幅を大きくしても、飛び出る電子の1個のエネルギーは一定なのです。
振動数を変えると飛び出る電子のエネルギーは変わるのです。

光が波であるとすると、この現象を説明することができません。

光は何なのでしょうか？
アインシュタインは、つぎのように仮定しました。

• 「光は粒子である」。
• 「1つ1つの粒子は、”振動数”と呼ばれている数値にプランク定数をかけた量のエネルギーを持っている」。

これを光量子仮説と呼びます。

光を粒子だとすれば光電効果の説明ができます。
光のエネルギーは（振幅ではなくて）振動数に関係するのです。
だから振動数が変われば飛び出る電子のエネルギーも変わるのです。

振動数ごとに、飛び出る電子の1個のエネルギーは決まっているのです。

光を強くする、ということは光の粒子を多くすることです。
光の粒子を多くすれば、飛び出る電子の個数も多くなります。結果として、大きいエネルギーが出てくることになるのです。

アインシュタインは光量子仮説の研究でノーベル賞を受賞しました。
（※相対性理論でノーベル賞を受賞したのではないのです。）

都市伝説では、「相対性理論は難しすぎてよく分からないから、光量子仮説にしておこう」ということだったようです。

結局、光は波なのか？　粒子なのか？

• 光の回折現象を説明するためには、光を波と考えなければなりません。
• 光の光電効果を説明するためには、光を粒子と考えなければなりません。

さて、一体、光の正体はどっちなのでしょうか？

先ほどすでに答えを言っていますが、両方なのです。

「そんなバカな」と思うかもしれません。
でもですね。これが量子の世界の現実なのです。

ここまでが1910年までのことです。

原子の世界（1910年から1920年代まで）

さて、光（電磁波）や電子を通じて量子という概念が誕生してきたことをここまで解説してきました。

そして、1910年代になると原子の形が分かってきました。

プランクやアインシュタインの説は最初多くの学者には半信半疑でした。
ところが、「量子の存在を前提で考えると、原子の内部構造も分かるのでは」という考えが誕生します。

それと同時に、また別な謎が出てきたのです。

原子の形

原子は中心に原子核があります。原子核の周囲には電子があります。

このことは、1897年、ジョセフ・ジョン・トムソン（イギリス）が発見していました。
その後の研究得も、全ての原子は構成要素として電子を含むということがあきらかになりました。
かつて、原子＝物質の最小単位、といわれてきた概念が置き換わったのです。

一方で、新しい謎が誕生します。

原子核と電子の配置がどのようになっているのか分かりませんでした。
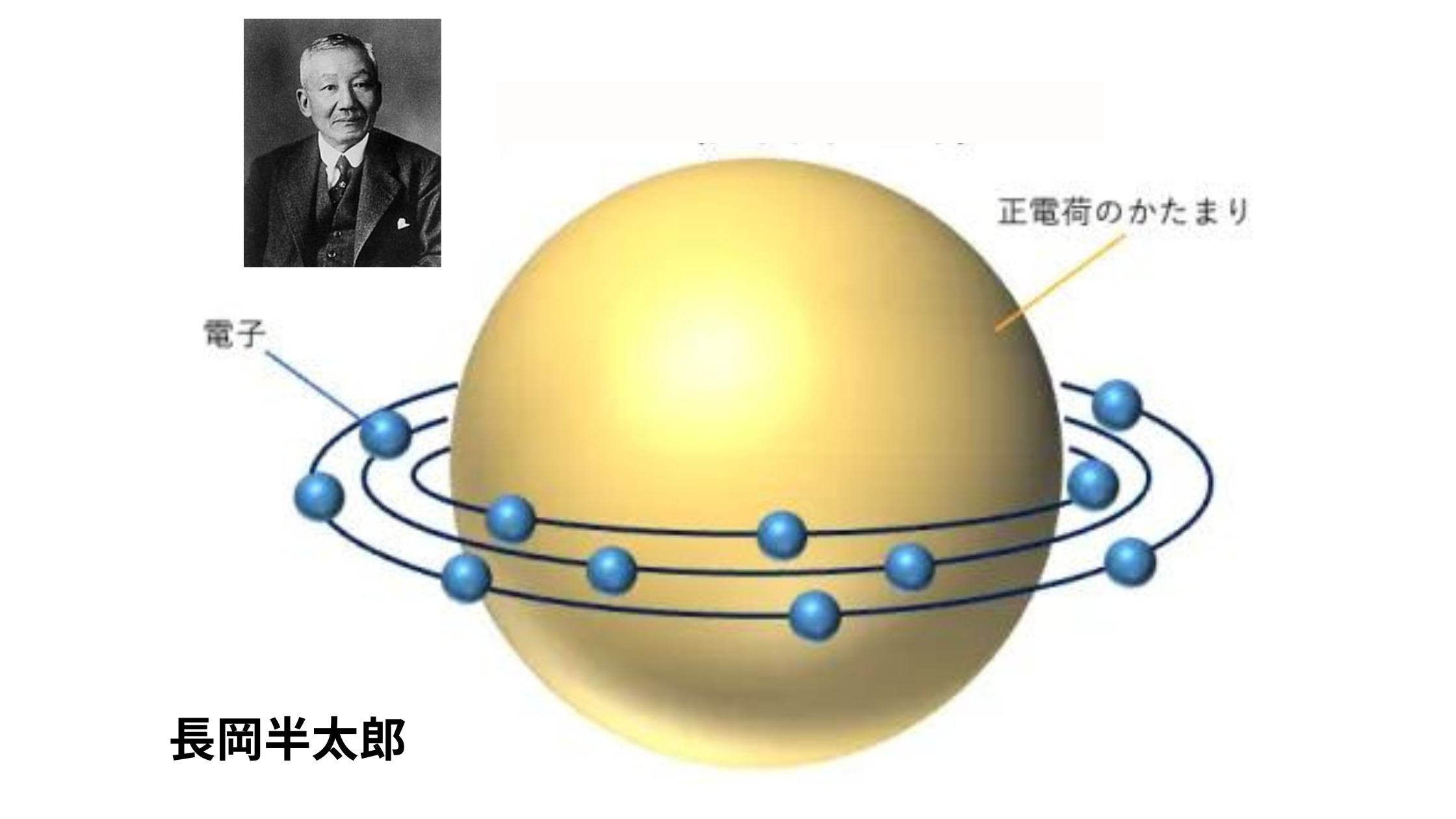
原子核の周囲に電子がぎっしりと詰まっているかもしれない、というモデルが考えられていました。
長岡半太郎（日本）は、土星のように、原子核の周囲を電子が輪を作っている、というモデルを提唱しました。

また、ラザフォード（イギリス）は、実験結果から、「原子は、太陽系のように、原子核の周囲を電子が回っているのだ」、と結論付けました。

電子の軌道

原子が太陽系のような形をしていることが分かると、すぐに疑問が出てきました。

電子が原子核を中心として円運動をしているなら、古典力学では、軌道の半径がゼロから無限大までのどの値を取ることができるのです。
そうすると、電子は電磁波を出しながら原子核へ落ちてしまうことになります。

これはありえないことです。
確かに電子は電磁波を出しています。そして同時に、原子は安定して存在しているのです。

どこがおかしいのでしょうか？

ニールス・ボーアの原子模型論（電子軌道の制限）

ニールス・ボーア

ボーア（デンマーク）は、電子の軌道には制限がある、と考えました。
「電子が原子核の周囲を公転するのはある条件を満たす半径の軌道の上だけなのだ」、としました。
この条件は量子条件と呼ばれています。

そして、公転しているときは電子のエネルギーは一定であり、ジャンプして軌道を変えるときに、電子は電磁波を出したり吸収したりする、と考えたのです。

ボーアの量子条件のポイントは、半径の数値は、連続ではなく、不連続な数値でなければならない、ということです。
不連続なところにプランク定数が関係しているのです。

ド・ブロイ（フランス）は、波の波長から電子の軌道を考えました。
「電子の波がピッタリとつながるような円周の長さのところにしか電子は存在できない」、ということです。
これは、極小粒子である電子の波の性質を使っています。

ボーアのモデルはラザフォードの考案した原子模型に、ド・ブロイの電子の量子性を融合させたものです。
ボーアモデルの前提はこうです。

ボーアの前のラザフォードモデルは古典物理学をベースとしており、電子がエネルギーを消失し原子核に向かって落ちてしまう（ハズ）という問題を抱えていました。

ところが、現実はそうはならない。

そこで、電子も量子であり不連続性があるものであるとし、プランクのエネルギー量氏の考え方を取り入れたのがボーアモデルです。

パウリの原理

電子の軌道を研究している最中に、パウリ（スイス）は、「同一の状態に電子はただ1つしか入ることができない」、ということに気が付きました。

これをパウリの原理といいます。

パウリの原理を使うことにより、元素の周期表の意味が明確に分かったのです。
原子や電子の構造が分かるにつれて、量子論の世界では”不連続”が重要な意味をもつ、と認識されるようになりました。

量子力学の世界（1920年代）

パウリの排他原理の登場に至るまでの間に、量子論で必要な概念が概ね整いました。

ここまでに、非常に微小な世界では、物質は、粒子の性質と波の性質の両方を持っていることが分かりました。
両方の性質を使わないと、いろいろな実験結果の説明ができないからです。

次の世代の研究者たちは、いろいろな実験結果の説明を統括するプロセスに入ります。
方程式やモデルを作り、古典力学では記述出来なかった量子の世界の出来事を、新しい力学として記述する研究がはじまります。

こうした物理学を量子力学といいます。

ハイゼンベルクの行列方程式

ヴェルナー・ハイゼンベルク

そして、量子力学の基盤を担った研究者の鏑矢ともなる人物が、ヴェルナー・ハイゼンベルク（ドイツ）。

今まで登場した人は変人ばかりですが、ハイゼンベルクもなかなかの方です。

まず、1920年、ゾンマーフェルトのもとで物理学を学ぶためミュンヘン大学へ。
そこで、前述のパウリと出会います。その後、ゲッティンゲンで、前述のニールス・ボーアに師事しました。
ある日、ボーアの講義の後、ハイゼンベルクは師のボーアと一緒に山登りをします。

その時、彼は、ボーアとの語らいの中で「原子はものではない！」という結論に至ります。
山登りから戻ってきたボーアは友人に「ハイゼンベルクは全てを理解している。」という言葉を残したそうです。

このようにボーアを師としたハイゼンベルクでしたがどうしてもボーアの原子模型論に登場する「想像上の電子軌道」が気に入らなかったそうです。

というのも、ハイゼンベルクは、「観測された事実、そして、観測されていない想像されたもの」を明確に区分する必要があると考えていました。ボーアの原子模型論では、電子が電磁波を放出・吸収する際にできる線スペクトルは観測事実です。一方で、原子核周囲の軌道を電子が回っているかどうかはわかりません（電子の軌道は想像されたに過ぎない）。

ハイゼンベルクは、悪性の花粉症を患いその治療を兼ねて北海のヘルゴラント島に行きます。
そこで、彼は、実験によって求められた光スペクトルの周波数と強度（明るさ）を、原子の中の量子数とエネルギー状態に結びつけるための鍵を探します。

彼は、この量子化された電子世界を記述する式を探索するなかで掛け算における基本的な法則が成り立たないことに悩まされました。

古典理論における掛け算は通常、交換法則があるためA×B＝B×Aが成り立ちます。
しかし、ハイゼンベルクは、自身の仮説を成り立たせるには、交換法則が成り立たない掛け算が必要だと気づいたのです。

自分の理論の中でスペクトル線の正しい周波数と強度を求めるため、師のボーアのように量子仮説を持ち込み、論文を書き上げます。

まず、その論文をパウリに見てもらいます。
さらに、ハイゼンベルクは論文をボルンにも見せます。
そして、その論文を読んだボルンは数学で言うところの「行列」の計算公式であることに気づきます。

行列は大学の数学で習うものです。
さすがの天才ハイゼンベルクも、物理学以外の大学の授業は忘れていたようです。
ボルンは、パスクアル・ヨルダンに協力を依頼し、ハイゼンベルクの行列公式に手直しを加え論文を発表します。

この時をもって、ニールス・ボーアの「量子論」が、本当の「量子力学」へと脱皮したと言えるでしょう。

シュレーディンガーの波動方程式

エルヴィン・シュレーディンガー

ハイゼンベルクの発見は画期的なものでした。
ただ、まだ、多くの課題が残されていました。

その最大の課題は、ハイゼンベルクの理論は行列力学であり、運用する視点では実用に難があったことです。
さらに、行列力学は量子世界の物理的現象につていて、「電子が軌道を回っている」というボーアやゾンマーフェルトのイメージを思い描くことを許容しない前提がありました。

このような状況から登場したのが、エルヴィン・シュレーディンガー（オーストリア）です。
彼は、ごく微小な世界を表す方程式にチャレンジしました。

シュレディンガーはド・ブロイの物質波の理論にヒントを見出します。
そして、電子が波として振る舞うのであればその波についての方程式を見つければいいじゃん！
という結論に至ります。

観測していないものは、

「ここにあるかもしれない」という「可能性」で存在しています。つまり、

「観測される前の量子（電子や原子）の位置は確率的に存在している」

ということです。

この確率は波の形で存在していることが二重スリット実験などで明らかになっています。
シュレディンガーはこの波の形を記述するための方程式を編み出しました。
それが、シュレディンガー方程式です。

1926年ハイゼンベルク等の論文が発表して間もないタイミングで、シュレディンガー方程式が発表されます。
これは電子が満たすべき方程式であり、シュレディンガー方程式を解けば、電子の波の形や変化を知ることができるようになったのです。

2つの方程式の等価性

量子世界を記述するのに、方程式が2つ出てきました。

1つはハイゼンベルクの行列力学。
そして、もう1つはシュレディンガーのシュレディンガー方程式。

2つの方程式は、どこがどう違うのだろうか？

このことについてシュレディンガーとパウリが研究してこう結論付けました。

「2つの方程式は同じ意味を表している、表現方法だけが異なっているのだ」

行列力学は量子の世界を「粒子（かたまり）」の視点で離散的に捉え、一方、波動力学は量子の世界を「波」の面から連続的に捉えたということです。
この違いを直感的に理解するならば、二重スリット実験が一番わかり易いでしょう。

量子理論に懐疑的な人々も、たくさんいました。
その1人がアインシュタインです。

量子の世界の理論（1920年代以降）

アインシュタインは、光電効果の解釈で量子論の発端を作りました。
量子論の最初の功労者の1人です。
それなのに、量子論の発展には納得がいきませんでした。

アインシュタインの言葉です。
「現象をとりあえず説明できたことは認めよう。でも、なにかがおかしい」。

アインシュタインは、多くの量子論学者に自分の疑問をぶつけていました。

そのピークとなったのが、第5回ソルベー会議です。

ソルベー会議

炭酸ナトリウムの製造で大富豪になったソルベーは科学のための国際会議を主催しました。

1927に開催された第5回ソルベー会議の議題は”電子と光子”で、そうそうたる物理学者たちが集まりました。

ちなみに、この時の集合写真が残っていますが、写っている29人のうち17人がノーベル賞受賞学者なのです。

ソルベー会議の最中、アインシュタインはボーアに量子論の問題点を指摘しました。

ボーアは、ホテルに帰って必死に答えを考えました。次の日、それをアインシュタインに伝えました。

アインシュタインは、また別の問題点を出します。ボーアは、それを考えて答えを出します。これのくり返しです。

パウリやハイゼンベルクも巻き込んで大論争となったのです。

この論争は1930年に開催された第6回ソルベー会議でも続きました。

これまでの論争を踏まえて、アインシュタインは自分の疑問点をEPR論文と呼ばれている論文に発表しました。

量子の世界の解釈（1920年代以降）

量子の世界についてはいろいろな解釈が考えられています。]

局所実在論

アインシュタインは局所実在論を信じていました。

局所性とは次のことです。
「ある場所で起きたことが他の場所に影響を及ぼすためには、光速以下の速度でなにかが伝わらなければならない」。
これは、アインシュタインなら当然考えることですよね。

実在論とは次のことです。
「なにかに影響を及ぼすことなく観測できる性質があるなら、観測していないときにもその性質は客観的である」。
アインシュタインは、「空を見上げたときだけ月があると君は信じるのかい？」と言っています。

不確定性原理

ハイゼンベルクは不確定原理を考案しました。
「位置と運動量を同時に正確に測定することはできない」、という原理です。

位置を正確に測定しようとすると運動量が大きくなるのです。運動量を正確に測定しようとすると位置が不正確になるのです。

たとえば、位置を測定しようとして光を当てると、その光のために運動量が増えてしまう、ということです。

それでは、光を当てて測定する前はどうなっているの？　という質問が飛んできますね。

つまり、実在論に関係する重要な問題が含まれているのです。

相補性原理

ボーアは不確定原理を拡張して相補性原理を考案しました。
「一方を決めると他方が不確定になる2つの量は相対立するものではなく、相補うものなのである」、ということです。

量子世界の電子や光は、観測手段によって粒子のようにも波のようにもふるまいます。
どちらが正しいのか、というのではなく、両方が相補って全体像になっているのだ、ということです。

コペンハーゲン解釈

不確定原理と相補性原理を根本に据えた量子論の考え方をコペンハーゲン解釈（または確率解釈）といいます。

「量子世界の電子や光は確率的に記述するしかない」、という解釈です。

「観測する前の状態は波動方程式で確率的に記述できて、観測したとたんに波動方程式は消滅して結果が出る」、ということなのです。

つまり、現在を正確に知ることは不可能であり、未来（結果）は確率的に分かるだけである、ということになります。

これは、古典物理学の因果律に反しています。
それで、アインシュタインは、「神はサイコロを振らない」と言いました。

シュレーディンガーの猫

コペンハーゲン解釈の有名なたとえとしてシュレーディンガーの猫というのがあります。

つぎのような思考実験です。
いま猫を箱の中に入れます。さらに原子を入れます。
原子が崩壊すれば猫は死にます。

ところで、原子の崩壊は量子論の世界の現象です。
原子の状態は波動方程式で確率的に記述できます。
原子は、崩壊と非崩壊の状態が重ね合っているのです。
簡単のために、原子が崩壊する確率は0.5だとします。
ということは、半分の確率で原子は崩壊するのですから、猫は半分だけ死んでいて、半分だけ生きていることになります。
そして、人間が箱を開けたとたんに、猫は生か死かに帰着するのです。

つまりは、量子の世界ではいろいろな状態が重ね合って存在している、ということなのです。
それが量子の世界なのだ、と量子論物理学者は信じるようになったのです。

でも、アインシュタインは、まだ納得がいきませんでした。

EPR論文

アインシュタインは、ボトルスキーとローゼンと一緒に、EPR論文と呼ばれるようになる論文を書きました。
量子論に対する疑問の総決算のような論文です。

アインシュタインは、いちばん気になっていることを繰り返しました。
局所性は必ず成立するはずだ、という主張です。
つまり、ある場所で起きたことが他の場所に影響を及ぼすためには、光速以下の速度でなにかが伝わらなければならない、ということです。

これにもボーアが反論しましたが、量子論をめぐる論争は下火になってきました。

量子の応用の方が盛んになってきました。
レーザーが発明され、集積回路からコンピュータが小型化され、我々の生活が便利になってきたのです。

むしろ、「存在とはどういうことなのか？」というような哲学的な議論が量子論を引き金として盛んになりました。

アインシュタインの過ち

アインシュタインは、量子論に懐疑的でした。

「現象をとりあえず説明できたことは認めよう。でも、なにかがおかしい」と思っていたのです。

量子論の方程式には”足りないもの”がある、と信じていたのです。
何かを加えれば局所性が成立するはずだ、と思っていました。

少し量子論から離れますが、アインシュタインは大きな過ちをしたことがあります。

1915年に一般相対性理論の方程式を作ったとき、”宇宙項”とよばれる項を加えました。
この項を加えないと、宇宙が変化してしまうのです。
アインシュタインは、宇宙は変化することはない、と信じていたのです。

しかし、1929年にハッブルが、宇宙は膨張していることを発見しました。

アインシュタインは、”宇宙項”を加えたことを、「わが生涯、最大の過ち」と悔やみました。

量子論の方程式では、アインシュタインが信じるように”足りないもの”があるのでしょうか？

量子の世界（続）（1960年代以降）

1960年代以降、物理学の流行は、量子論の応用へ移りました。
でも、理論物理学者は、量子論の探求を続けていました。

多世界解釈

ヒュー・エヴェレット

コペンハーゲン解釈では、観測したとたんに波動方程式は消滅することになっていました。
ですから、波動方程式そのものが存在することも分からないのです。

これに対して、ヒュー・エヴェレット（アメリカ）は、「波動方程式は現実に存在する」、と考えました。
波動方程式は無限に存在するのですが、ということは、波動方程式が記述する世界も無限に存在することになります。

いろいろな世界が無限に多く存在するのです。
SF作家が喜びそうな理論ですね。

多世界解釈を使うと、EPR論文で問題になっていた局所性は解決されます。
量子の世界でも局所性は成立することになるのです。

ベルの不等式

1964年にベル（北アイルランド）は局所性に関する不等式を作りました。

「物理理論が局所性を持っているなら、その理論の式はプラスマイナス2の範囲に収まる」、という関係式です。

量子論でベルの不等式を計算すると、プラスマイナス2.8になります。
プラスマイナス2の範囲を超えてしまう、ということでおおさわぎになりました。

量子論では局所性が壊れてしまう、ということです。

それとも、量子論が不十分なのでプラスマイナス2の範囲を超えたのでしょうか。

量子論が正しいのか？　量子論が不十分なのか？

どちらなのか、実験で調べるしかありません。

ベルの不等式の検証

1972年にフリードマン（アメリカ）とクラウザー（アメリカ）は、実験で量子の世界ではプラスマイナス2の範囲を超えることを確かめました。

1982年にアスペ（フランス）が、さらに精密な実験をして間違いないことが分かったのです。

量子論ではベルの不等式は成立しないのです。

局所性の否定

量子の世界ではプラスマイナス2の範囲を超えてしまうので、量子の世界では局所性が壊れてしまう、ということになります。

つまり、なにかが光速を超えて瞬時に伝わるのです。
SF作家が喜びそうなことですね。

アインシュタインは局所性にこだわり、”足りないもの”があると信じていました。
じつは、足りないものはありませんでした。
量子の世界は、局所性を超えた世界だったのです。

量子論の応用（2024年から未来へ）

これから先、量子論はどうなるのでしょうか？

通信革命

光速を超えて瞬時に伝わるなら情報伝達に使えます。
電話線も光ケーブルも必要なくなります。
しかも途中で盗み見される心配がありません。

通信手段の大革命が起きますよ。

量子コンピュータ

現在のコンピュータは、0か1か、という二者択一の論理で作られています。
量子の世界では0と1の間の数字を取ることができるので、これを論理に据えれば、超高速のコンピュータを作ることができます。
現在のコンピュータでは1万年かかる計算が3分で終了するのです。

桁違いなスピードですね。

さらに先へ

量子論は、アインシュタイン、ボーア、ハイゼンベルクなどの天才たちが作り上げました。

現在でも、多くの天才がいます。
彼らが量子論の開拓を続けています。

これまで以上に驚くべき世界を見せてくれるでしょう。
そして、我々の生活を豊かにしてくれるのです。

まとめ

量子論は光や電子の研究から始まりました。

光や電子が活躍する微小な世界は、普通の常識とは異なる世界であることが分かりました。

天才たちの血のにじむような努力と新しい世界観を知ると、勇気と活力がわいてきますね。

我々の現在の豊かな生活は、物理学者たちの理論と、それを形にした技術者たちのおかげなのです。

もちろん、量子論には、まだまだ研究しなければならない事がたくさん残っています。
物理学者が失業することはないのです。